Video Overview
Introduction
The charge q on a capacitor’s plate is proportional to the potential difference V across the capacitor. We express this relationship with
where C is a proportionality constant known as the capacitance. C is measured in the unit of the farad, F, (1 farad = 1 coulomb/volt).
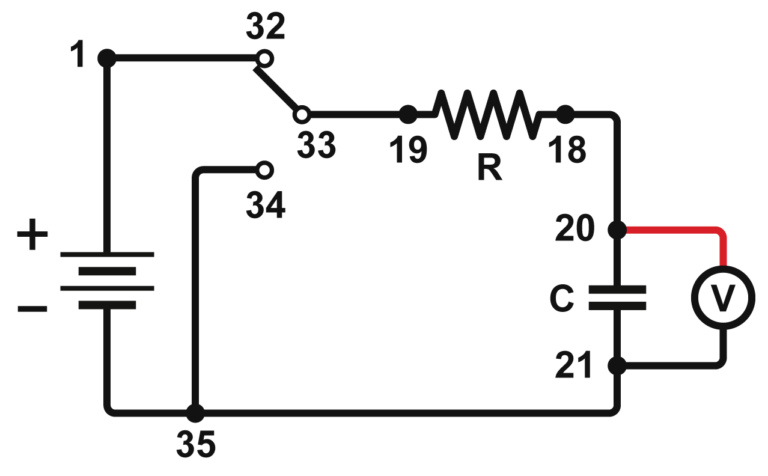
If a capacitor of capacitance C (in farads), initially charged to a potential V0 (volts) is connected across a resistor R (in ohms), a time-dependent current will flow according to Ohm’s law. This situation is shown by the RC (resistor-capacitor) circuit below when the switch is connecting terminals 33 and 34.
As the charge flows, the charge q on the capacitor is depleted, reducing the potential across the capacitor, which in turn reduces the current. This process creates an exponentially decreasing current, modeled by
The rate of the decrease is determined by the product RC, known as the time constant of the circuit. A large time constant means that the capacitor will discharge slowly.
In contrast, when the capacitor is charged, the potential across it approaches the final value exponentially, modeled by
The same time constant, RC, describes the rate of charging as well as discharging.
Objectives
- Measure an experimental time constant of a resistor-capacitor circuit.
- Compare the time constant to the value predicted from the component values of the resistance and capacitance.
- Measure the potential across a capacitor as a function of time as it discharges and as it charges.
- Fit an exponential function to the data. One of the fit parameters corresponds to an experimental time constant.
Sensors and Equipment
This experiment features the following sensors and equipment. Additional equipment may be required.
Correlations
Teaching to an educational standard? This experiment supports the standards below.
- International Baccalaureate (IB)/Physics
- 11.3 Capacitance
Ready to Experiment?
Ask an Expert
Get answers to your questions about how to teach this experiment with our support team.
- Call toll-free: 888-837-6437
- Chat with Us
- Email support@vernier.com
Purchase the Lab Book
This experiment is #24 of Physics with Vernier. The experiment in the book includes student instructions as well as instructor information for set up, helpful hints, and sample graphs and data.
