How does Logger Pro calculate velocity and acceleration from Motion Detector data?

Logger Pro and Graphical Analysis calculate derivatives numerically.

Depending on the number of points used for derivatives (you can set this value in the settings for that file, found under the File menu), the derivative and secondderivative functions use 3, 5, 7, ,,n points to estimate the slope of a tangent line. Note that the software does not ever find slopes by successive differences of only two points.

The number of points used for finding derivatives has a major impact on the appearance of velocity graphs. Using more points will smooth out irregular features, but will also smear out useful detail if taken too far. See TIL 2331: How do I adjust the number of points used in derivative calculations?

If the target is a person, it is helpful to use lots (11 to 15) points for derivatives; in contrast, that many points for a ball toss experiment will result in smeared out velocity and acceleration graphs.

The slope itself is calculated as a weighted average of slopes from points on either side of the target point. For example, suppose we have a portion of a data table of (t, x) pairs, and we want the derivative at row i:

t[i-2] x[i-2]
t[i-1] x[i-1]
t[i] x[i]
t[i+1] x[i+1]
t[i+2] x[i+2]

for n=3, the derivative at row i is

(x[i+1] - x[i-1])/(t[i+1] - t[i-1])

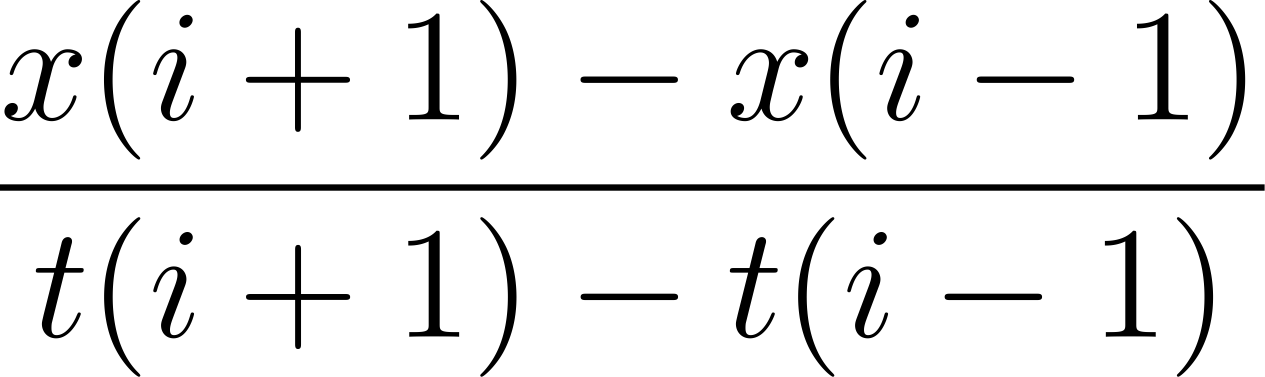
That is, the change in x divided by the change in time, using the rows on either side of row i.

for n=5, the additional i+2 and i-2 rows are used:

((x[i+2] - x[i-2])/(t[i+2] - t[i-2]) +
2*((x[i+1] - x[i-1])/(t[i+1] - t[i-1]))/3

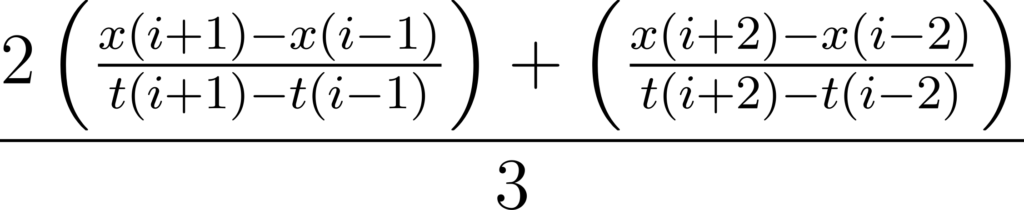
That is, the derivative using five rows is the weighted average of the slopes found from the rows just before and after row i, two rows before and after, etc.
For n=5, the weights are 2 and 1. For n=7, the weights are 3, 2 and 1.

The second derivative is the same algorithm applied twice.

There is also an option of the SG, or Savitzky-Golay derivatives. These are more complex calculations, but they will sometimes preserve the shape and magnitude of derivatives more than the former method. Often the two methods give virtually the same result, however.

See also:
TIL 1141: How does Logger Pro calculate velocity and acceleration from photogate data?