Video Overview
Introduction
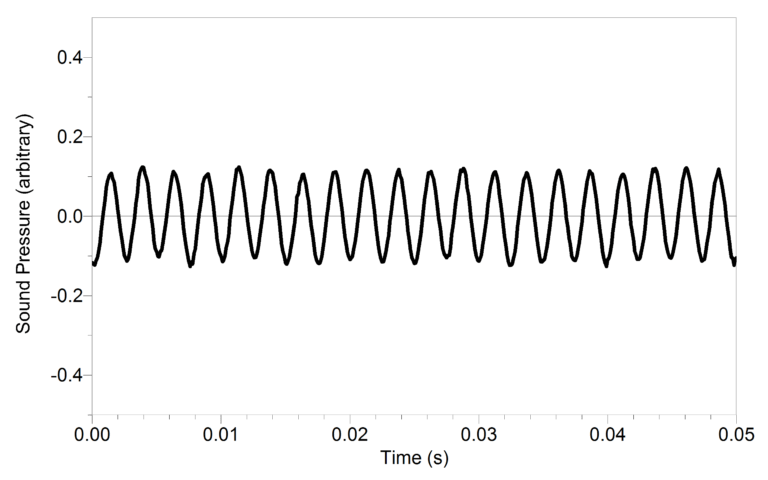
Sound waves consist of a series of air pressure variations. A Microphone diaphragm records these variations by moving in response to the pressure changes. The diaphragm motion is then converted to an electrical signal. Using a Microphone and an interface, you can explore the properties of common sounds.
The first property you will measure is the period, or the time for one complete cycle of repetition. Since period is a time measurement, it is usually written as T. The reciprocal of the period (1/T) is called the frequency, f, the number of complete cycles per second. Frequency is measured in hertz (Hz). 1 Hz = 1 s–1.
A second property of sound is the amplitude. As the pressure varies, it goes above and below the average pressure in the room. The maximum variation above or below the pressure mid-point is called the amplitude. The amplitude of a sound is closely related to its loudness.
In analyzing your data, you will see how well a sine function model fits the data. The displacement of the particles in the medium carrying a periodic wave can be modeled with a sinusoidal function. Your textbook may have an expression resembling this one:
In the case of sound, a longitudinal wave, y refers to the change in air pressure that makes up the wave, A is the amplitude of the wave, and f is the frequency. Time is represented by t, and the sine function requires a factor of 2π when evaluated in radians.
When two sound waves overlap, air pressure variations will combine. For sound waves, this combination is additive. We say that sound follows the principle of linear superposition. Beats are an example of superposition. Two sounds of nearly the same frequency will create a distinctive variation of sound amplitude, which we call beats.
Objectives
- Measure the frequency and period of sound waves from a keyboard.
- Measure the amplitude of sound waves from a keyboard.
- Observe beats between the sounds of two notes from a keyboard.
Sensors and Equipment
This experiment features the following sensors and equipment. Additional equipment may be required.
Option 1

Option 2

Ready to Experiment?
Ask an Expert
Get answers to your questions about how to teach this experiment with our support team.
- Call toll-free: 888-837-6437
- Chat with Us
- Email support@vernier.com
Purchase the Lab Book
This experiment is #32 of Physics with Vernier. The experiment in the book includes student instructions as well as instructor information for set up, helpful hints, and sample graphs and data.

