Attention: Safety Recall of Vernier Go Direct Charge Station. Click to learn more.
Menu

Shop

  • Experiment
  • From Here to There – Applications of the Distance Formula

Experiments​

From Here to There – Applications of the Distance Formula

Experiment #13 from Real-World Math with Vernier

Education Level
High School

Introduction

Many problems in applied mathematics involve finding the distance between points. If we know the coordinates of a pair of points (x1, y1) and (x2, y2), it is easy to find the distance between them by using the distance formula, which is a restatement of the Pythagorean Theorem.

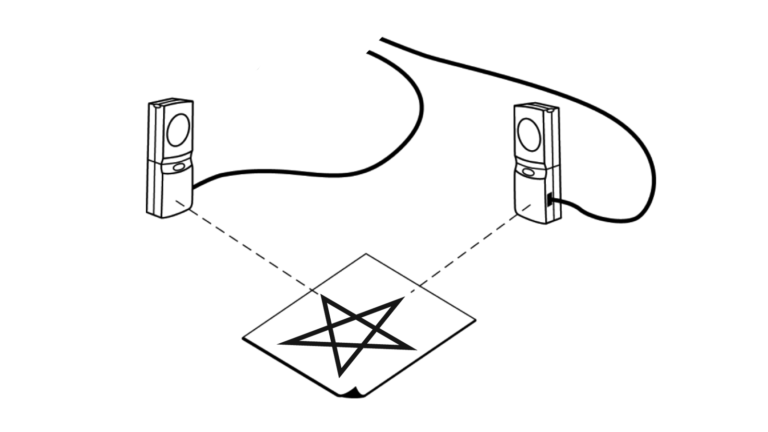
d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}

In this activity you will use a pair of Motion Detectors. They will record the Cartesian x, y coordinates of a rod moving in a star-shaped pattern. The data collected by the detectors will be used to test the distance formula.

Objectives

  • Record the x– and y-coordinates of a rod moving in a star pattern.
  • Use the recorded coordinates to calculate the distances moved between the vertices of the star.
  • Compare the calculated distances with direct measurement on the star pattern.

Sensors and Equipment

This experiment features the following sensors and equipment. Additional equipment may be required.

Option 1

Motion Detector (2)
Meter Stick

Option 2

CBR 2 (2)
Meter Stick

Ready to Experiment?

Ask an Expert

Get answers to your questions about how to teach this experiment with our support team.

Purchase the Lab Book

This experiment is #13 of Real-World Math with Vernier. The experiment in the book includes student instructions as well as instructor information for set up, helpful hints, and sample graphs and data.

Learn More

SAVE/SHARE YOUR CART