Stepping to the Greatest Integer: The Greatest Integer Function
Experiment #31 from Real-World Math with Vernier
- Education Level
- High School
Introduction
Not all mathematical functions have smooth, continuous graphs. In fact, some of the most interesting functions contain jumps and gaps. One such function is called the greatest integer function, written as y = int x. It is defined as the greatest integer of x equals the greatest integer less than or equal to x. For example, int 4.2 = 4 and int 4 = 4, while int 3.99999 = 3.
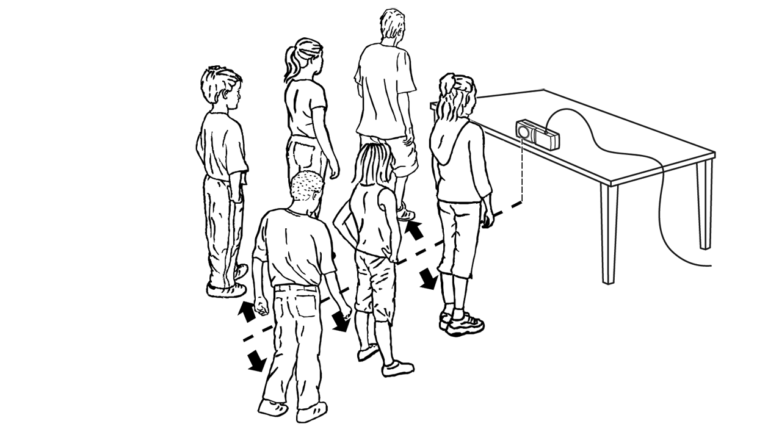
In this activity, you will create a function similar to the greatest integer function graph by having a group of students stand in a line in front of a Motion Detector and then step aside one by one. The equation for this graph, in the general form, is
You can find appropriate values for the parameters A, B, and C so that the model fits the data.
Objectives
- Use a Motion Detector to collect position data showing evenly-spaced jumps in value.
- Model the position data using the greatest integer function.
Sensors and Equipment
This experiment features the following sensors and equipment. Additional equipment may be required.
Ready to Experiment?
Ask an Expert
Get answers to your questions about how to teach this experiment with our support team.
- Call toll-free: 888-837-6437
- Chat with Us
- Email support@vernier.com
Purchase the Lab Book
This experiment is #31 of Real-World Math with Vernier. The experiment in the book includes student instructions as well as instructor information for set up, helpful hints, and sample graphs and data.




