Expression Details

  • An expression must be a number, a data column, an appropriately formatted function, or a combination of these items: [5, “X”, sin(“X”), 5sin(“X”)]
  • Column names must be entered with quotes. [sin(“X”), “Y”, or abs(“Z”)]
  • Supported operators are + – * / ^ ( )
  • Functions must contain their arguments in parentheses. [abs(“X”) or sqrt(2)]
  • Multiplication can be explicit or implied. [5*“X”, 5“X”, or 5(“X”)]
  • Constants must be entered as numbers. Variable parameters (e.g., A, B, C) are not supported.
  • Trigonometric functions are evaluated in radians.
  • Functions can be nested as long as the proper format is used. [sqrt(abs(“X”))]

Function Syntax

Analysis Functions

Function Syntax Description
analysis analysis(“X”,startRow,endRow)

analysis(“X”,2,4)

 Aggregates data from the specified rows of a column named ‘X’ (from all data sets) into a single column of data.
dataSets dataSets(“X”,startRow,endRow)

dataSets(“X”,2,4)

 Creates a column where the row values are the data set names from which the aggregated data was acquired.

Analysis functions aggregate data from multiple datasets into a single column.
● X—the name of the column from which data is to be copied
● startRow—first row from which data is to be copied
● endRow—last row from which data is to be copied

Blood Pressure Functions

Function Syntax Description
diastolic diastolic(“Pressure”,”Time”) The measured arterial pressure when the heart is at rest.
meanArterialPressure meanArterialPressure(“Pressure”,”Time”) The pressure value at the max peak used for calculating blood pressure.
oscillations oscillations(“Pressure”,”Time”) Oscillations of the peaks and valleys used for calculating blood pressure.
oscillatoryPeaks oscillatoryPeaks(“Pressure”,”Time”) Relative maximum values from the oscillations data used to calculate systolic, diastolic, and pulse values.
pulse pulse(“Pressure”,”Time”) Pulse rate calculated using the blood pressure sensor inputs.
systolic systolic(“Pressure”,”Time”) The measured arterial pressure when the heart contracts.

“Pressure” and “Time” are columns from data collection with a Blood Pressure Sensor (BPS-BTA) or Go Direct® Blood Pressure Sensor (GDX-BP).

Boolean Expressions

Operator Syntax Description Examples
AND “X” AND “Y” True (1) if BOTH inputs are True, otherwise False (0). 1 AND 1 = 1
1 AND 0 = 0
0 AND 1 = 0
0 AND 0 = 0
NOT (!) ! “X” True (1) if the input is False. False (0) if the input is True. ! 1 = 0
! 0 = 1
OR “X” OR “Y” True (1) if AT LEAST one input is True, otherwise False (0). 1 OR 1 = 1
1 OR 0 = 1
0 OR 1 = 1
0 OR 0 = 0
XOR “X” XOR “Y” Exclusive OR
True (1) if ONLY one input is True, otherwise False (0).		 1 XOR 1 = 0
1 XOR 0 = 1
0 XOR 1 = 1
0 XOR 0 = 0

A Boolean expression is either True (1) or False (0) based on the operator and value of the inputs. When the inputs are columns, the output is a column where Boolean values are determined row-by-row.

  • Input value = False (0) when the input is…
    ⚬ a number = 0 (must identically equal zero, not just round to zero)
  • Input value = True (1) when the input is…
    ⚬ any number ≠ 0
    ⚬ Any non-numeric value (including text string = 0)
    ⚬ Empty column cells

Operators can be combined (e.g., “X” AND ! “Y”, ! “X” OR “Y”, and ! “X” XOR ! “Y” are valid expressions).

Calculus Functions

Function Syntax Description
firstDerivative firstDerivative(“Y”,“X”,numberOfPoints)

firstDerivative(“Position”,“Time”)
firstDerivative(“Position”,“Time”,3)

 Finds the first derivative of data in column ‘Y’ with respect to column ‘X’. ‘numberOfPoints‘ is set in Session Preferences or can be explicitly set. Default = 7
integral integral(“Y”, “X”) Numerical integral – the running sum of the areas of rectangles calculated using the midpoint rule. The ith rectangle is identified by [Yi – Y(i-1)] and [Xi – X(i-1)]
secondDerivative secondDerivative(“Y”,“X”,numberOfPoints)

secondDerivative(“Position”,“Time”)
secondDerivative(“Position”,“Time”,3)

 Finds the second derivative of data in column ‘Y’ with respect to column ‘X’. ‘numberOfPoints‘ is set in Session Preferences or can be explicitly set. Default = 7

Derivative and Integral function parameters:
● Y—a column of data you want to differentiate or integrate
● X—the independent variable column for your data; typically Time
● numberOfPoints—[closest] odd integer ≥ 3 (Session Preference options: 3 ,5, 7, 9, 11, 15, or 21)

For more information on derivative calculations, see How do Logger Pro, Graphical Analysis, LabQuest app, and Vernier Video Analysis calculate velocity and acceleration?

Collapse Functions

Function Syntax Description
collapse collapse(“X”) Creates a new column equivalent to column ‘X’ with the blank cells removed.
collapseIndirect collapseIndirect(“X”,”Y”) Creates a new column containing values from only the rows in column ‘X’ that correspond to the rows in column ‘Y’ that are numbers (skipping rows where column ‘Y’ has blank cells).

Collapse functions are used to remove empty cells from columns and to retain correlations between data from other columns (that do not include empty cells). This is helpful when wanting to use functions such as delta() and sum() with columns that contain empty cells.

Column-Fill Functions

Function Syntax Description
constant constant(constant,count) This function generates a column with every cell value = ‘constant’.
randInt randInt(min,max,count) This function generates a column of random integers between the values of ‘min’ and ‘max’ (inclusive).
randReal randReal(min,max,count) This function generates a column of random real numbers between the values of ‘min’ and ‘max’ (inclusive).
rowNumber rowNumber() This function generates a column of values where the cell value is the row number of the cell. (This function has no arguments.)
step step(start,increment,count, firstRow,skip) Generates a column having ‘count’ rows. The first reported value is ‘start’ and subsequent values are increased or decreased by the value of the ‘increment’. ‘firstRow’ defines the row in which the first value is reported. ‘skip’ defines is the number of rows skipped between reported values.
stepColumnBased stepColumnBased(“X”,start, increment,firstRow,skip) This function is similar to the step function, except output values will appear only in non-empty rows in column ‘X’. ‘firstRow’ = 2 corresponds to the second non-empty row of column ‘X’. ‘skip’ = 1 will report output values in every other non-empty row of column ‘X’.
  • The data table needs to have active rows in the data set for the fill-value functions to work. These functions do not create active rows automatically.
  • The number of rows in the output column is determined by the value of ‘count‘; however, the value is limited by the number of active rows in the dataset.
  • When ‘count‘ is a column (e.g., ‘X’), the value of ‘count‘ is number of rows in column ‘X’.

Column-Manipulation Functions

Function Syntax Description
abs abs(arg1) absolute value (|x|)
delta delta(“X”) The difference between consecutive values from column ‘X’. (The ith value of the output is ith value of ‘X’ minus the (i-1)th value of ‘X’.) The output will have an empty first row.
interpolate interpolate(“Y”,”X”) This function generates a column where missing values in the ‘Y’ column are filled in using linear interpolation. Column ‘X’ is the independent variable, typically Time.
rms rms(“X”) Cumulative Root Mean Square of the values in column ‘X’ up to the current row. The output value reported for row 3 is sqrt((X12+X22+X32)/3))
subset subset(“X”,start,step) Returns a column of data extracted from column ‘X’ starting with the row numbered ‘start’, incremented by ‘step’ rows. Rows in column ‘X’ that are skipped are blank in the output column.
sum sum(“X”) The sum of the values in column ‘X’ up to the current row. The output value reported for row 3 is the sum of the column ‘X’ values from rows 1, 2 and 3.
value value(offset,”X”) Creates a new column based on column ‘X’ by extracting values from column ‘X’ that are ‘offset’ rows from the current row.
offset = -2 has column ‘X’ row 1 copied to output row 3 with the first two rows of the output blank.
offset = 2 has column ‘X’ row 3 copied to output row 1 with the last two rows of the output blank.
offset = 0 will have an output that duplicates column ‘X’.

Function parameters:
● X and Y—are columns of data
● arg1—can be a number, an expression that resolves to a number, or a column of numbers (“X”).
● offset, start, and step—are integers

Digital Filter Functions

Function Syntax Description
bandPassFilter bandPassFilter(“Y”,“X”,bandPassRipple, lowCutoff,highCutoff)

bandPassFilter(“Signal”,“Time”,0.5,1, 50)

 Filter data that have unwanted FFT frequencies outside two ‘cutoff’ values. For EKG/EMG data, filter frequencies below 1 Hz to remove noise from arm or leg movements, and filter frequencies above 50 hz to remove noise from a US power supply.
bandStopFilter bandStopFilter(“Y”,“X”,bandPassRipple, lowCutoff,highCutoff)

bandStopFilter(“Potential”,“Time”,0.5,50,70)

 Filter data that have unwanted FFT frequencies between two ‘cutoff’ values. For voltage data, use a 50 to 70 Hz band stop filter to remove noise from a US power supply.
highPassFilter highPassFilter(“Y”,“X”,bandPassRipple,cutoff)

highPassFilter(“Signal”,“Time”,0,1)

 Filter data that have unwanted FFT frequencies below the ‘cutoff’ value. For EMG data, use a 1 Hz high pass filter to remove noise from muscle movements such as a twitch.
lowPassFilter lowPassFilter(“Y”,“X”,bandPassRipple,cutoff)

lowPassFilter(“Signal”,“Time”,0,50)

 Filter data that have unwanted FFT frequencies above the ‘cutoff’ value. For EKG data, use a 50 Hz low pass filter to remove noise from a power supply affecting your data.
timeDecayFilter timeDecayFilter(“Y”,“X”,timeDecay) Use this function to apply a time decay to the data.

Digital Filter functions are designed to work with analog sensors and/or truly analog signals. Signals or sensors that perform digital signal processing may not work well with these features.

  • Y—the column of data to which the filter is being applied
  • X—the independent variable column for your data; typically Time
  • bandPassRipple—This value is the percentage of pass-band
    ⚬ Low Pass and High Pass filters are typically 0, which applies a Butterworth filter
    ⚬ Band Stop and Band Pass filters are typically 0.5, which applies a Chebyshev filter
    ⚬ To mimic an analog filter circuit, set the bandPassRipple to 0
    ⚬ In most cases, a bandPassRipple set to 0.1 will give the best results
  • cutoff, lowCutoff, highCutoff—the FFT frequency cutoff value used for the filter; must be a number
  • timeDecay—time decay constant, typically in seconds

Energy Sensor Functions

Function Syntax Description
energy energy(“Potential”,”Current”) Calculates Energy in Joules (J)
power power(“Potential”,”Current”) Calculates Power in milliwatts (mW)
resistance resistance(“Potential”,”Current”) Calculates Resistance in ohms (Ω)

“Potential” (measured in V) and “Current” (measured in mA) are columns from data collection with a Vernier Energy Sensor (VES-BTA) or Go Direct® Energy Sensor (GDX-NRG).

Exponential and Logarithmic Functions

Function Syntax Description Examples
exp exp(arg1) Natural (base-e) exponential function (ex) exp(2) ≈ 7.389
exp2 exp2(arg1) base-2 exponential function (2x) exp2(2) = 4 
expm1 expm1(arg1) ex–1 or exp(x)–1
Greater accuracy for ‘x’ values close to 0.
Inverse of log1p(x).		 expm1(0.005)
≈ 0.005012521
ln ln(arg1) Natural or base-e logarithmic function 
(ln x or loge x)		 ln(2.719) ≈ 1
log log(arg1) common or base-10 logarithmic function
(log x or log10x)		 log(1000) = 3
log1p log1p(arg1) ln(1+x)
Greater accuracy for ‘x’ values close to 0.
Inverse of expm1(x)		 log1p(0.005012512)
≈ 0.005
log2 log2(arg1) base-2 logarithmic function (log2x) log2(8) = 3

● arg1—can be a number, an expression that resolves to a number, or a column of numbers (“X”).

Modulo (Integer Remainder) Functions

Function Syntax Description Examples
mod mod(arg1,arg2) Modulo – integer remainder of X/Y
mod(x,y) = x – y*trunc(x/y)		 mod(5,4) = 1
mod(6,4) = 2
mod(7,4) = 3
remainder remainder(arg1,arg2) ISEE – integer remainder of X/Y
remainder(x,y) = x – y*round(x/y)		 remainder(5,4) = 1
remainder(6,4) = -2
remainder(7,4) = -1

● arg1—can be a number, an expression that resolves to a number, or a column of numbers (“X”).

Photogate and Projectile Launcher Functions

Projectile Launcher Functions

Function Syntax Description
Gate Time DEPLGateTime(“Time”,”Gate State”,”Gate State”) Calculates the time between the first blocked event and the next unblocked event.
Launch Speed DEVelocity(“X”,distance)

DEVelocity(“Pulse Time”,0.05)
DEVelocity(“Gate Time”,0.017247)

 Calculates the Launch Speed of the projectile using as ‘distance’ either the projectile launcher’s photogate separation and the pulse time, or the projectile’s diameter and the gate time.
Pulse Time DEPLPulseTime(“Time”,”Gate State”,”Gate State”) Calculates the time between the first two blocked events.
Time of Flight DEPLTimeOfFlight(“Time”,”Gate State”,”Gate State”) Calculates the time between the first blocked event and the third blocked event.

The inputs for these calculations are the Gate State and Time columns from Vernier Projectile Launcher (VPL) or Go Direct® Projectile Launcher (GDX-PL). The projectile launcher’s photogates and optional Time of Flight Pad (TOF-VPL) are the equivalent of two (or three) photogates daisy-chained together.

Single Photogate

Linear and Angular Motion

Function Syntax Description
firstDerivative TimeShift
(Velocity)		 firstDerivativeTimeShift(“Distance”,”Time”) Used to find Velocity from Distance and Time data.
secondDerivative TimeShift
(Acceleration)		 secondDerivativeTimeShift(“Distance”,
“Time”)		 Used to find Acceleration from Distance and Time data.
stepColumnBased
(Distance)		 stepColumnBased(“X”,start,increment,
firstRow,skip)

Linear Motion—Picket Fence
(“Gate State”,0,0.05,1,1)

Linear Motion—Cart Picket Fence
(“Gate State”,0,0.01,1,1)

Angular Motion—10-spoke pulley
(“Gate State”,0,0.6283,1,1)

 Used to generate Distance data from Gate State data.

X—Gate State column
start—initial distance (= 0)
increment—distance traveled between blocked events
firstRow—which non-empty row in Gate State column to start from
skip—number of non-empty Gate State rows to skip for next value

Gate State, Distance, and Time columns are from data collection with wired Photogate (VPG-BTD) or from data collection with Go Direct® Photogate (GDX-VPG) setup to use Gate State sensor channels.

Single Photogate Functions

Speed Through Gate, Timing, Pendulum Timing

Function Syntax Description
Blocked to Blocked Times
(Pulse Time)		 DEBlockToBlock(“Time”,”Gate State”,”Gate State”) Calculates the time between successive blocked events.
Blocked to Unblocked Times
(Gate Time)		 DEBlockToUnblock(“Time”,”Gate State”,”Gate State”) Calculates the time between a blocked event and the next unblocked event.
Pendulum Period DEPendulumPeriod(“Time”,”Gate State”,”Gate State”) Calculates the time between every second blocked event (after the first blocked event).
Speed Through Gate DEVelocity(“X”,distance)

DEVelocity(“Gate Time”,0.05)
DEVelocity(“Pulse Time”,0.02)

 Calculates the speed by dividing the blocking object’s width (‘distance’) by the Gate Time. If using Pulse Time, ‘distance’ is how far the object travels between blocked events.

Gate State and Time columns are from data collection with wired Photogate (VPG-BTD) or from data collection with Go Direct® Photogate (GDX-VPG) setup to use Gate State sensor channels.

Two Photogate Functions

Function Syntax Description
Blocked to Blocked Time
(Pulse Time)		 DEBlockToBlock(“Time”,”Gate State 1″,”Gate State 2″) Calculates the time between a blocked event on Gate 1 and the next blocked event on Gate 2. (Gate 1 must be blocked before Gate 2).
Speed Between Gates DEVelocity(“X”,distance)

DEVelocity(“Pulse Time”,0.10)

 Calculates the speed by dividing the ‘distance’ between the photogates by the Pulse Time.

Gate State and Time columns are from data collection with wired Photogate (VPG-BTD) or from data collection with Go Direct® Photogate (GDX-VPG) setup to use Gate State sensor channels.

Use these functions to calculate typical photogate measurements when collecting time-based data.

Power Functions (xn)

Function Syntax Description Examples
cbrt cbrt(arg1) cube root cbrt(27) = 3
pow pow(arg1,arg2) power (xy)
x = arg1 and y = arg2		 pow(5,3) = 125
power(3,5) = 243
sqrt sqrt(arg1) square root sqrt(81) = 9

● arg1—can be a number, an expression that resolves to a number, or a column of numbers (“X”).

Rate and Beats Per Minute Functions

Function Syntax Description
rate rate(“Y”,”X”,t,m1,m2,n,dt)

rate(“Signal”,”Time”,15,0.4,0.6,0,5)

 The rate of column ‘Y’ with respect to column ‘X’, where t is the time interval measured, ‘m1’ is min percentage threshold, ‘m2’ is max percentage threshold, ‘n’ is noise threshold, and ‘dt’ is the offset to start of the next range.
beatsPerMinute beatsPerMinute(“Y”,”X”,t,m1,m2,n,dt) This function is similar to the rate function except that the interval (‘t’) is in seconds and the output values are in minutes.
If column ‘X’ is in seconds, then beatsPerMinute(“Y”,”X”) = 60*rate(“Y”,”X”)

● Y—a column of data for which you want to determine the rate of oscillation
● X—the independent variable column for your data; typically Time

Rounding Functions

Function Syntax Description Examples
ceiling ceiling(arg1) Nearest integer greater than a given number. ceiling(3.5) = 4
ceiling(-3.5) = -3
floor floor(arg1) Nearest integer less than a given number. floor(3.5) = 3
floor(-3.5) = -4
integer integer(arg1) Integer part of a given number.
interger(arg1) = trunc(arg1)		 interger(3.5) = 3
interger(-3.5) = -3
round round(arg1) Rounds to the nearest integer.
When the decimal value of ‘arg1’ is exactly 0.5, values are rounded up if ‘arg1’>0 and rounded down if ‘arg1′<0.		 round(3.5) = 4
round(-3.5) = -4
trunc trunc(arg1) Truncate – Integer part of a given number.
trunc(arg1) = interger(arg1)		 trunc(3.5) = 3
trunc(-3.5) = -3

● arg1—can be a number, an expression that resolves to a number, or a column of numbers (“X”).

Smoothing Functions

Function Syntax Description
smoothAve smoothAve(“Y”) This function returns a column of moving averages of the values in column ‘Y’. ‘numberOfPoints’ is set in Session Preferences. Default = 7
smoothSG smoothSG(“Y”,”X”,numberOfPoints)

smoothSG(“Position”,“Time”)
smoothSG(“Position”,“Time”,3)

 Savitsky-Goley smoothing fits a polynomial to a number of points around each point and computes the value of the polynomial at that point. ‘numberOfPoints’ is set in Session Preferences or can be explicitly set. Default = 7

Smoothing functions.
● Y—is the columns of numbers you want to smooth
● X—the independent variable column for your data; typically Time
● numberOfPoints—[closest] odd integer ≥ 3 (Session Preferences: 3 ,5, 7, 9, 11, 15, or 21.)

Statistical Functions

Function Syntax Description
max max(“X”) Reports the largest number in column ‘X’.
max2 max2(“X”,”Y”)
max2(“X”, 5)		 Compares the values in column ‘X’, row by row, with values in column ‘Y’ (or some constant) and reports the larger of the two numbers for the corresponding row in the output column.
mean mean(“X”) Arithmetic mean of the numbers in column ‘X’.
median median(“X”) The median (middle) value of the ranked (ordered) values in column ‘X’. Column ‘X’ does not need to be sorted.
min min(“X”) Reports the smallest number in column ‘X’.
min2 min2(“X”,”Y”)
min2(“X”,5)		 Compares the values in column ‘X’, row by row, with values in column ‘Y’ (or some constant) and reports the smaller of the two numbers for the corresponding row in the output column.
numRows numRows(“X”) This outputs the number of rows in column ‘X’.
rms rms(“X”) Cumulative Root Mean Square of the values in column ‘X’ up to the current row. The output value reported for row 3 is sqrt((X12+X22+X32)/3))
stddev stddev (“X”) The standard deviation of the numbers in a column ‘X’.

● X and Y—are columns of numbers
● arg1—can be a number, an expression that resolves to a number, or a column of numbers (“X”).

Trigonometric Functions

Hyperbolic Trigonometric Functions

Function Syntax Description Examples
acosh acosh(arg1) inverse hyperbolic cosine acosh(2)≈1.317
asinh asinh(arg1) inverse hyperbolic sine asinh(1)≈0.4812
atanh atanh(arg1) inverse hyperbolic tangent atanh(0.5)≈0.5493
cosh cosh(arg1) hyperbolic cosine cosh(1.317)≈2
sinh sinh(arg1) hyperbolic sine sinh(0.4812)≈1
tanh tanh(arg1) hyperbolic tangent tanh(0.5493)≈0.5

● arg1—can be a number, an expression that resolves to a number, or a column of numbers (“X”).

Standard Trigonometric Functions

Function Syntax Description Examples
acos acos(arg1) arccosine or inverse cosine (output in radians) acos(0.5)≈1.047
asin asin(arg1) arcsine or inverse sine (output in radians) asin(0.5)≈0.5236
atan atan(arg1) arctangent or inverse tangent (output in radians) atan(1)≈0.785
atan2 atan2(arg1,arg2) 2-argument arctangent — The angle (in radians) between the x-axis and a line connecting the origin and the point (x,y) atan2(4,3)≈0.927
atan2(3,4)≈0.644
cos cos(arg1) cosine (‘arg1’ in radians) cos(1.407)≈0.5
sin sin(arg1) sine (‘arg1’ in radians) sin(0.5236)≈0.5
tan tan(arg1) tangent (‘arg1’ in radians) tan(0.785398)≈1

● arg1—can be a number, an expression that resolves to a number, or a column of numbers (“X”).

● Trigonometric functions are evaluated in radians.

Miscellaneous Functions

Function Syntax Description Examples
copysign copysign(arg1,arg2) Changes the sign of a number to match the sign of another number copysign(-5,1)=5
copysign(5,-2)=-5
dim dim(arg1,arg2) Calculates the difference between two numbers and reports the value if the difference is ≥ 0; otherwise reports 0. dim(10,8) = 2
dim(10,9.9) = 0.1
dim(8,10) = 0
erf erf(arg1) error function or Gauss error function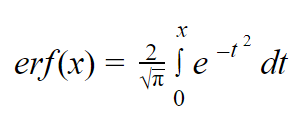
 erf(.25) ≈ 0.276
erfc erfc(arg1) Complementary error function
erfc(x) = 1 – erf(x)		 erfc(.25) ≈ 0.724
hypot hypot(arg1,arg2) Hypotenuse
hypot(x,y) = sqrt(x2 + y2)		 hypot(5,12) = 13
hypot(4,3) = 5
logb logb(arg1) floating-point base logarithmic function, logb(x), returns the unbiased exponent value of ‘x‘ as a signed integer represented as a floating-point value.
logb(arg1) = floor(log2(abs(arg1)))		 logb(10) = 3
logb(-1.5) = 0
logb(0.1) = -4
nextafter nextafter(arg1,arg2) Computes next representable float after X in the direction of Y nextafter(1/0,1)=infinity
PolarRadius PolarRadius(arg1,arg2) Finds r when coverting cartesian to polar coordinates (x,y) → (r,θ)
r = sqrt(x2 + y2) = hypot(x,y)		 PolarRadius(1,1)≈1.414
PolarTheta PolarTheta(arg1,arg2) Finds θ when coverting cartesian to polar coordinates (x,y) → (r,θ)
θ = atan(y/x); 0 ≤ θ < 2π radians		 PolarTheta(1,1)≈0.785

● arg1—can be a number, an expression that resolves to a number, or a column of numbers (“X”).

Related Links

Published: February 24, 2021. Updated: April 15, 2025.