How would you make a derivative machine? Here’s an unexpected way:
Faraday’s law states that there is an induced emf in a coil, proportional to the time rate of change of the magnetic flux Φ through that coil, or
where N is the number of turns in the coil.
You can do this experiment with a LabQuest, a Power Amplifier, an Instrumentation Amplifier, and a set of nesting coils. We used a common coil set that is often used with galvanometer experiments. The Vernier Power Amplifier steps up low-current and low-voltage signals from the LabQuest for driving larger loads. In particular, to create magnetic fields large enough to easily detect, currents on the order of hundreds of milliamps are required. The Power Amplifier is perfect for this application.
The Power Amplifier app on the LabQuest is used to set the output. For example, one can select a triangle wave at 1 V peak-to-peak amplitude with a frequency of 25 Hz. This can be applied to a primary coil. A smaller, secondary coil resides inside the primary coil. The Instrumentation Amplifier is a voltage sensor for signals as small as 20 mV. In this experiment, it is used to detect the induced emf in the secondary coil.
In the spirit of modeling good classroom technique, let’s make a prediction. The current flowing in the primary coil is in the form of a triangle wave. The time derivative of a triangle wave, with constant positive and negative slopes, is a square wave. The frequency would be the same as the driving triangle wave.
What really happens? Here are some sample data.
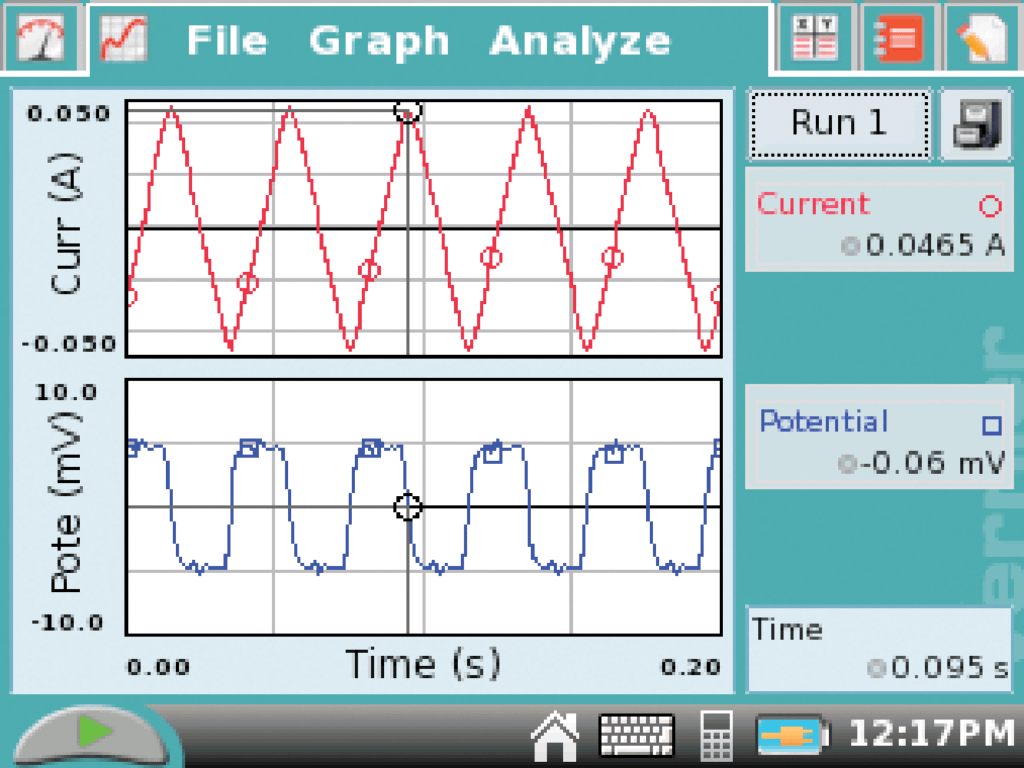
As expected, the induced emf, shown in the lower graph, is a square wave.
Some questions to have your students consider:
- What will happen if the drive frequency is increased?
- What will happen if the drive amplitude is changed?
- What will happen if the drive waveform is changed to a sine wave?
