Introduction
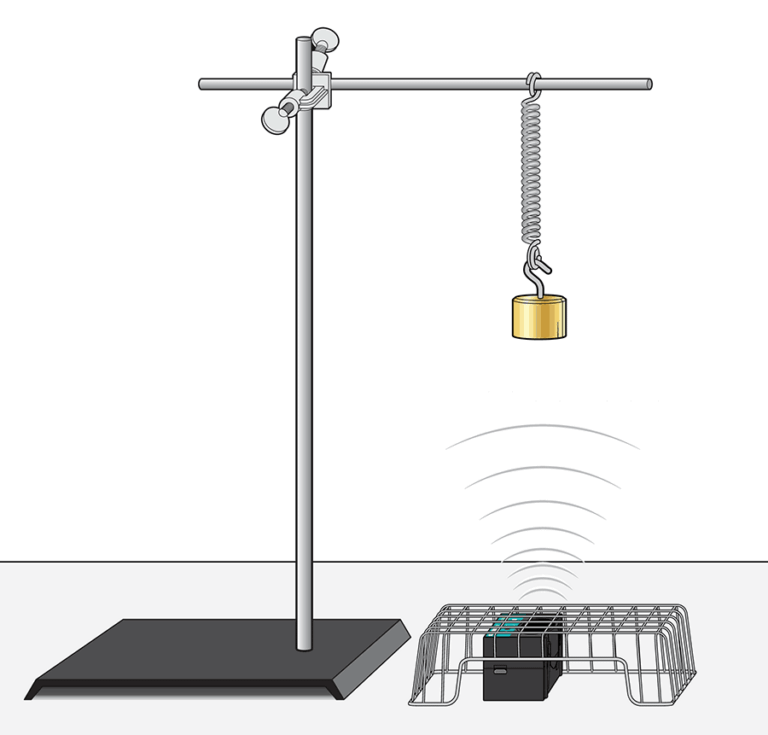
When you suspend an object from a spring, the spring will stretch. If you pull on the object and release it, it will begin to oscillate up and down. In this experiment, you will examine this kind of motion, perform a curve fit on the position-time graph, and relate the parameters of the equation with physical features of the system.
Objectives
In this experiment, you will
- Collect position vs. time data as a mass, hanging from a spring, is set in an oscillating motion.
- Determine the best fit equation for the position vs. time graph of an object undergoing simple harmonic motion (SHM).
- Define the terms amplitude, offset, phase shift, period and angular frequency in the context of SHM.
- Relate the parameters in the best-fit equation for a position vs. time graph to their physical counterparts in the system.
- Use deductive reasoning to predict the system mass required to produce a given value of angular frequency in the curve fit to SHM.
